Virgola mobile, problema fisso
Poche cose sono sicure: alcuni esempi sono le tasse, la morte, e il fatto che i computer diano risultati assolutamente precisi quando si tratta di fare calcoli. A dirla tutta, le tasse non sono così sicure secondo il Ministero dell’Economia, visto che si stima un’evasione fiscale di oltre 100 miliardi di euro nel 2018. Anche sulla morte potremmo non essere tanto certi: sono state scoperte delle forme di vita che non muoiono mai, semplicemente giunte a una certa età regrediscono a uno stato infantile e poi crescono di nuovo, e si sta studiando un modo per fare la stessa cosa almeno con alcuni organi umani. I computer, almeno, sono affidabili. Forse. È un periodo storico pieno di incertezze.
Se si tratta di fare calcoli è ovvio che un computer sia molto più bravo e e veloce di un essere umano. Ma questo non significa che sia del tutto preciso. Prima o poi anche un computer deve approssimare, e questo per il semplice motivo che le risorse di memorizzazione non sono infinite. Con i numeri irrazionali, come il Pi Greco oppure i periodici, non si può avere precisione: dopo un certo numero di cifre decimali bisogna fermarsi e arrotondare. Di solito questa approssimazione non è un problema, ma se si fanno milioni di calcoli e le approssimazioni di tanti numeri si sommano è possibile che il risultato finale di una operazione risulti sbagliato. Ma forse è meglio fare un passo indietro. All’origine, i computer potevano capire solo i numeri interi. Ancora oggi il processore più semplice da realizzare è uno in grado soltanto di sommare e sottrarre numeri interi. La soluzione più economica per gestire i numeri con virgola è usare una notazione che prevede la virgola fissa. Si tratta di una soluzione in voga con i calcolatori elettromeccanici, e in realtà si usa tutt’ora (solo come forma di scrittura) in molti documenti contabili: viene definito un numero fisso di cifre dopo la virgola e tutti i numeri vengono scritti con quelle cifre anche se non ne hanno bisogno. Se si legge uno scontrino e tutti i prezzi hanno due cifre decimali è molto facile fare una somma o una differenza mentalmente, perché le cifre sono allineate in base al loro valore (centesimo, decimo, unità, decina, eccetera). È una cosa che si vede anche su display molto semplici, che hanno un numero fisso di cifre e quindi una virgola fissa, come quelli delle pompe per la benzina.

Per capire il problema del floating point in codice binario basta pensare a come procedono le potenze di due
A un certo punto ci si è resi conto che bisognava trovare un altro modo per scrivere i numeri, assicurandosi di poter esprimere qualsiasi numero almeno con una approssimazione decente. Questa cosa era un problema soprattutto per gli scienziati, che dovevano fare calcoli con numeri reali (numeri con la virgola) di diverse dimensioni, alcuni con molti decimali e altri con pochi. Il difetto del sistema a virgola fissa è la poca versatilità. È per questo nasce il sistema floating point, o “virgola mobile”. Che poi non è altro che la notazione scientifica. La regola è semplice: a sinistra della virgola c’è solo una unità, cioè la prima cifra del numero da sinistra. Tutte le altre si trovano dopo la virgola, e per risalire all’effettivo ordine di grandezza del numero si moltiplica tutto per un esponente di 10 (o per la base in cui si sta lavorando, nel caso del codice binario la base è 2). È una cosa molto più semplice a farsi che a dirsi, come molti aspetti della matematica: il numero
1234
diventa
1,234*10^3
mentre il numero
25193,476
diventa
2,5193476*10^4
oppure, con una forma di scrittura abbastanza comune
2,5193476E+4
e il numero
0,08462
diventa
8,462E-2
Come si può intuire, si tratta di un sistema molto flessibile, perché basta memorizzare tutte le cifre del numero, e poi memorizzare anche la posizione della virgola come potenza di dieci.
Il problema è che questo tipo di calcoli è complicato da gestire per un computer. Sembra strano: per noi è incredibilmente facile. Se vogliamo calcolare a mente il prodotto
300000 * 0,002
basta considerare le notazioni esponenziali, cioè
3E5 * 2E-3
e diventa ovvio che il risultato sia
6E2
Però per un computer le cose non sono così semplici. Per gestire nativamente i calcoli con la virgola mobile serve una apposita unità del processore, nota come Floating Point Unit, che come tutte le cose in più è ovviamente un costo. Il computer a bordo dei razzi delle missioni Apollo non era in grado di usare la virgola mobile, perché sarebbe costato troppo: tutti i calcoli che richiedevano l’uso di virgola mobile venivano svolti a terra e il risultato inviato nello spazio. Oggi è ormai abbastanza comune, però esistono ancora processori ARM a 32 bit o meno che non supportano il floating point hardware (o hard float). Questi devono ricorrere al soft float, cioè una emulazione software dell’unità floating point. Il soft float è ovviamente più lento, almeno un centinaio di volte più lento, ma continuerà a esistere perché non tutte le operazioni matematiche (soprattutto le meno comuni) sono implementate a livello hardware per la virgola mobile.
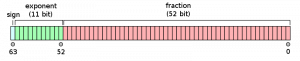
In un sistema a 64bit si usano 52 bit per indicare le cifre e 11 bit per la posizione della virgola, più uno per il segno
Si aggiunge un ulteriore problema: avendo un numero fisso di cifre disponibili, quando si calcola con dei numeri irrazionali prima o poi bisogna approssimare. Per esempio, su sistemi a 32 bit ci sono 23 bit per memorizzare le cifre in formato binario, e il resto serve per memorizzare la posizione della virgola. Se si hanno più di queste cifre, le rimanenti vanno approssimate. E a forza di approssimare prima o poi si otterrà un risultato del tipo
2+2 = 4,000000000001
Questo avviene perché nel sistema binario il valore decimale 0,1 è un numero periodico e deve essere approssimato. Infatti
DEC 0,1 = BIN 0,00011001100110011...
I bit dopo la virgola non rappresentano infatti un decimo, un centesimo, un millesimo, eccetera. Si riferiscono a un mezzo, un quarto, un ottavo. E non si può scrivere 0011 all’infinito avendo solo 23 bit. Se la notazione scientifica è quindi perfettamente funzionale in ogni caso nella base 10, non è perfetta in base 2. E i computer possono essere costretti a fare una approssimazione sull’ultima cifra dei decimali. Quindi in alcune occasioni il computer potrebbe dirci che l’affermazione
0,1+0,2 == 0,3
è falsa, perché facendo la somma ottiene in realtà 0,29999 oppure 0.300001. Se stiamo eseguendo un programma con una istruzione if otterremo un errore, e sarà un floating point error. Nella maggioranza dei casi non è un problema, ma se si sta scrivendo un programma che deve calcolare il bilancio di uno stato o le transazioni economiche tra grandi aziende, un errore apparentemente piccolo può trasformarsi in un grande buco economico. La soluzione è quindi fare tutti i calcoli usando numeri interi, ricordandosi poi di dividere il risultato in base all’ordine di grandezza corretto. Questo perché il limite è dato proprio dal codice binario, che non permette di esprimere tutti i decimali. Un computer si comporta più o meno al contrario di un bambino distratto: si applica, ma non ha le potenzialità.




